11月16日晚,山东大学金融研究院研究员何勇博士应邀为amjs澳金沙门线路首页全体研究生及导师开展主题为“Matrix Kendall’s tau in High-dimensions: A Robust Statistic for Matrix Factor Model”的学术讲座。活动采取线上形式进行,由amjs澳金沙门线路首页刘广应教授主持,学院全体研究生及导师参加。
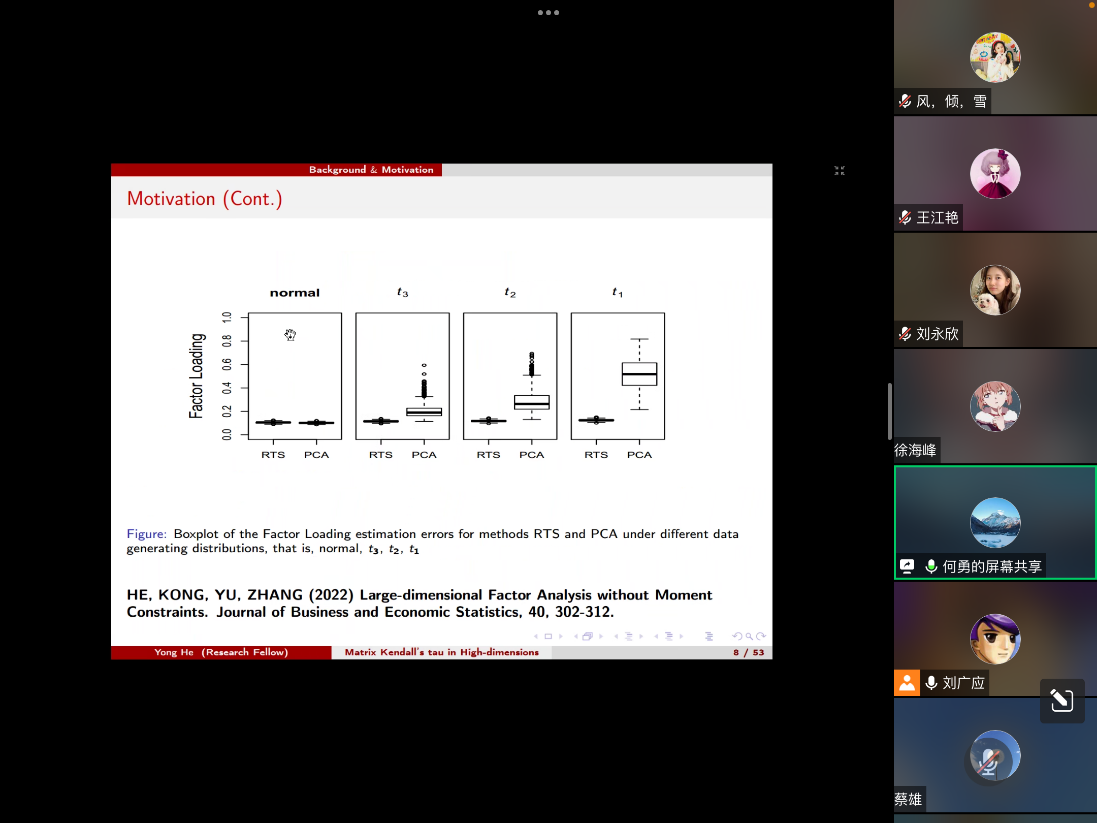
在报告中,何勇博士主要介绍了Kendall’ s tau矩阵应用于矩阵因子模型的原理、实例与拓展,对广义行/列矩阵Kendall’s tau进行特征值分解,以恢复矩阵因子模型的加载空间。首先,何勇博士为我们介绍了向量因子模型,并通过不同数据生成分布的因子负荷估计误差说明尾部变厚时,PCA方法会变差,但是RTS方法很稳健。同时解释了椭球分布族和椭球因子模型,并列举不同国家的不同宏观经济指标与典型矩阵数据如核磁共振数据来说明。对于遵循矩阵变量椭圆轮廓分布的随机矩阵,所提出的行/列矩阵Kendall’s tau的特征空间分别与行/列散射矩阵的特征空间一致,具有相同的特征值降序。然后何勇博士介绍了矩阵因子模型,提出若想实现稳健则可以利用Huber损失,并且在考虑稳健的估计方法时可以借助Spatial Kendall’s Tau方法,并详细地介绍了最小二乘方法和Huber方法。最后,根据上述理论性质进行实例模拟,结果表明本文提出的估计方法比现有估计方法具有更高强度的稳健性,并在扩展中说明希望可以考虑Tensor的椭球分布。
会议最后,与会师生何勇博士进行了热烈的交流互动,研究生院副院长孔新兵教授与何勇博士就该报告中影像数据、Tensor投影、CP分解方法与数据是否为矩阵椭球等问题交流意见,并期望以后能有更深入的相互学习和交流的机会。通过本次讲座,与会师生均表示受益良多,对于矩阵因子模型与Kendall’s Tau方法有了新的认知。

